文章地址：https://www.usenix.org/system/files/sec20summer_gu_prepub.pdf
标题：PCKV: Locally Differentially Private Correlated Key-Value Data Collection with Optimized Utility
作者：Xiaolan Gu, Ming Li, Yueqiang Cheng, Li Xiong, Yang Cao
发表会议：USENIX20

Introduction
Related Work
Preliminaries
- Local Differential Privacy
- Mechanisms under LDP
Key-Value Data Collection under LDP
- Problem Statement
- PrivKVM
Proposed Framework and Mechanisms
- Sampling Protocol
- Perturbation Mechanisms
- Aggregation and Estimation
- Optimized Privacy Budget Allocation
Evaluation
- Synthetic Data
- Real-Wrold Data
Conclusion

这篇文章做的工作和 PrivKV 那篇是一样的，参考 PrivKV 那篇文章的连接：http://forestneo.com/2019/03/25/%E8%AE%BA%E6%96%87%E9%98%85%E8%AF%BB-PrivKV/

Introduction

前两段引入了 LDP 和 Key-Value data 的概念。然后指出了什么是 KV 数据中的频率估计和均值估计，以图1为例，每个数据表示用户对电影的评分，那么频率估计就是估计每部电影评分的数目，均值估计就是估计每部电影的平均评分。

KV 数据中是有着一定挑战的：1. 某个用户是拥有多个 KV 数据的，这就意味着如果要把 epsilon 分配给每个 KV 对，那么每个 KV 对的 epsilon 就会很小，导致误差很大。2. Key 和 Value 之间有着一定的联系，单单把 key 和 value 用已有的方法去实现 LDP 效果不是特别好。

在 KV 数据的估计上，PrivKVM 是目前首先提出的方法。其有三个主要的缺陷。1. 需要迭代多轮以达到理论上的无偏，这会导致方差偏大。2. 其用了一个sampling protocol，每个用户从总的 Key Space 采样一个 key 进行 perturb，这也会导致误差。3. 没有一个系统的方法研究 epsilon 在 key 和 value 上的组合特性。

本文提出了一个新的框架：PCKV，Locally Differentially Private Correlated Key-Value。可以从四个方面对 PrivKVM 进行提升。

我们提出了更好的均值估计方法，并且不需要迭代。
我们使用了更先进的 sampling protocol。
我们表明，对 KV pair 的 privacy budget 比将 key 的和 value 的 privacy budget 加起来要低。
由于我们的方案可以直接分析出频率估计和均值估计的 MSE，我们可以更好地对 key 和 value 分配 privacy budget。

总的来说，本文的贡献如下：

我们提出了 PCKV 框架，同时提出了两种方法：PCKV-UE，基于 unary encoding，PCKV-GRR，基于 generalized randomized response。我们的方法是 non-interactive的，我们理论上分析了误差，并且我们的方法是几乎无偏的。
我们扩展了 padding-and-sampling 协议使其适用于 key-value 数据，这比 PrivKVM 中的采样协议更好。
我们展示了 key-value 中的 budget composition。
我们为 PCKV-UE 和 PCKV-GRR 提出了渐进最优的 privacy budget分配方案。
我们用生成的数据集和公开的数据集表明我们方案拥有更好地估计效果，同时也印证我们理论分析的正确性。

这部分略过了。

Preliminaries

Local Differential Privacy

LDP 的定义如下：

$\frac{\operatorname{Pr}(\mathcal{M}(x)=y)}{\operatorname{Pr}\left(\mathcal{M}\left(x^{\prime}\right)=y\right)} \leqslant e^{\varepsilon}$

Mechanisms under LDP

这里讲了几个背景知识，分别是RR，GRR，UE，以及其方差。RR接触的很多了，就不介绍了。

GRR，generalized randomized response，工作原理如下：

$\operatorname{Pr}(\mathcal{M}(x)=y)=\left\{\begin{array}{ll}{p=\frac{e^{\varepsilon}}{e^{\epsilon}+ d-1},} & {\text { if } y=x} \\ {q=\frac{1-p}{d-1},} & {\text { if } y \neq x}\end{array}\right.$

UE，Unary Encoding，工作原理如下：

$\operatorname{Pr}(\mathbf{y}[k]=1)=\left\{\begin{array}{ll}{p,} & {\text { if } \mathbf{x}[k]=1} \\ {q,} & {\text { if } \mathbf{x}[k]=0}\end{array} \quad(\forall k=1,2, \cdots, d)\right.$

UE当中分为 SUE 和 OUE，SUE 中，$p=\frac{e^\epsilon}{e^\epsilon+1}, q=1-p$，OUE 中 $p=\frac{1}{2},q=\frac{1}{e^\epsilon+1}$。其对频率估计的方差为：

$\operatorname{MSE}_{\hat{f}_{i}}=\operatorname{Var}\left[\hat{f}_{i}\right]=\frac{q(1-q)}{n(p-q)^{2}}+\frac{f_{i}^{*}(1-p-q)}{n(p-q)}$

Key-Value Data Collection under LDP

Problem Statement

问题定义从系统模型、威胁模型和目标和挑战三个层次说明。

系统模型。如图1所示，假定用户集合为 $\mathcal{U}$, 大小为 $|\mathcal{U}|=n$。每个用户有一系列 KV 对 $\langle k, v \rangle$，其中 $k \in \mathcal{K}, v\in \mathcal{V}$，我们假定 Key 和 Value 的值域为 $\mathcal{K}=\{1,2, \cdots, d\}, \mathcal{V}=[-1,1]$。我们用 $S$ 表示一个用户的 KV 对集合，用户 $u$ 的为 $S_u$。然后有一个数据收集者收集了这些数据然后想要计算出每个 key 的频率和均值，定义如下：

$f_{k}^{*}=\frac{\sum_{u \in \mathcal{U}} \mathbb{1}_{S_{u}}(\langle k, \cdot\rangle)}{n}, \quad m_{k}^{*}=\frac{\sum_{u \in \mathcal{U},\langle, v\rangle \in \mathcal{S}_{u}} v}{n \cdot f_{k}^{*}}$

其中 $\mathbb{1}_{\mathcal{S}_{u}}(\langle k, \cdot\rangle)$是1当$\langle k, \cdot\rangle \in \mathcal{S}_{u}$，否则为0。

威胁模型。我们假定数据收集者是不可信的，然后每个用户只信任自己。

目标和挑战。目标就是在满足一定隐私条件情况下估计频率和均值。然而这也是不容易的，由于以下几点：1）每个用户是由多个 KV 对的。一方面，如果每个用户需要对所有的 KV 对编码的话，每个 KV 对的 privacy budget 就会很小。另一方面，如果从 $\mathcal{K}$ 中随机采样一个 key，并且 perturb 这个 $\langle k, v \rangle$ 对（PrivKVM就是这么做的），用户的数据可能得不到充分使用。2）Key 和 Value 之间是有联系的，Perturb 的过程中也需要考虑这种联系。3）由于key 和 value 的相关性，对 key-value 对的 privacy budget 可能比加起来要少。

PrivKVM

PrivKVM 的算法流程，参考之前写的文章描述。这里主要说一下 PrivKVM 的三个主要缺陷：

为了达到理论上的无偏估计，其采用了多伦迭代的方式，这导致每一轮的 privacy budget 非常小，者会带来大的方差。
其采用的 sampling protocol 过于简单，由于每个用户的 key-value 对较少，很可能采样的是无效的。
尽管其考虑了 key 和 value 之间的关联，其并没有优化 key-value 中的组合性质。

Proposed Framework and Mechanisms

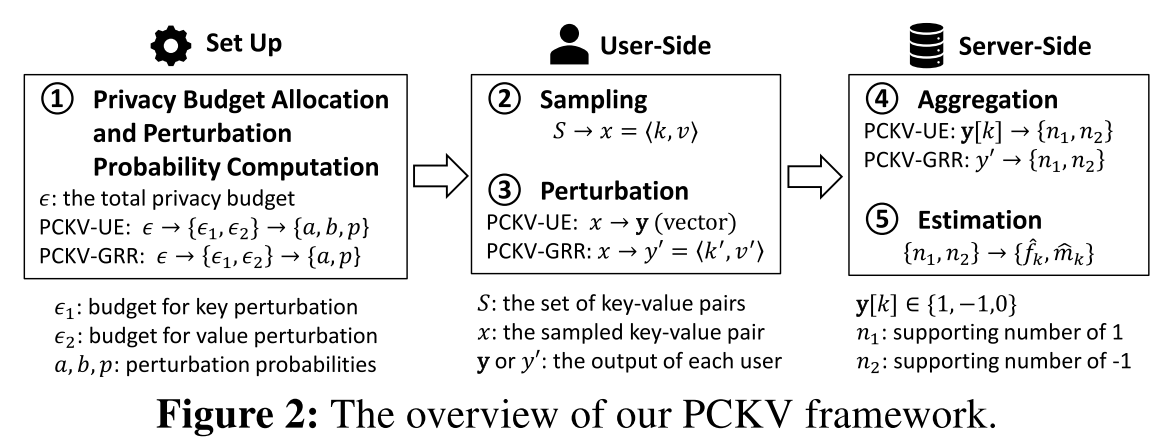
总的来说，本文的方案如图2所示，其中包含两种方法：PCKV-UE 和 PCKV-GRR。PCKV-UE 的输出是 a bit vector，PCKV-GRR的输出是 a key-value pair。总体而言流程大致相同，细节来看，134对应不同的方法。

Sampling Protocol

这一节对应图2中的第二步。假定用户有多个 Key-Value pairs，我们一般不会去 perturb 所有的KV对，而是有一个采样（Sampling）的操作，只选一个进行 Perturb。

本文采用的采样过程叫做 Padding-and-Sampling 协议，来源于论文[23]。用户从已有的 KV pair中选取一个进行采样，而不是从 Key Space中选取一个。为了使得采样的可能性对不同的用户来说相同，每个用户首先将自己的 KV 对进行一个 padding 操作。这个过程如算法1所示。

即以概率 $\eta=\frac{|S|}{\max \{|\mathcal{S}|, \ell\}}$ 从 $S$ 里面随机采样，以剩下的概率从采样一个 dummy KV pair。根据这个采样算法，当用户的 pair 数目很大的时候，直接从用户的 pair 里面采样，当用户的数据量很小的时候，以一定的概率从用户那里采样。因此，这个随机采样的方案比 PrivKVM 中的要好。

那么 $\ell$ 如何选取呢，根据[23]，较小的 $\ell$ 会低估频率导致较大的偏差，较大的 $\ell$ 会使得方差更大。（这句话读的时候有疑问）。但是如何科学地设定 $\ell$ 的值目前还是没有方法的，因此本文选取了一些 reasonable 的值来和 PrivKVM 比较。至于怎么科学选取 $\ell$ 就留给 future work了。

Perturbation Mechanisms

这部分对应图2的第三步。根据算法1，我们已经 sample 了一个 KV pair，表示为：$x = \langle k, v \rangle$，其中 $k\in \mathcal{K’}, v \in [-1,1]$。然后介绍两个机制：PCKE-UE 和 PCKV-GRR。我们先来说 PVKV-UE。

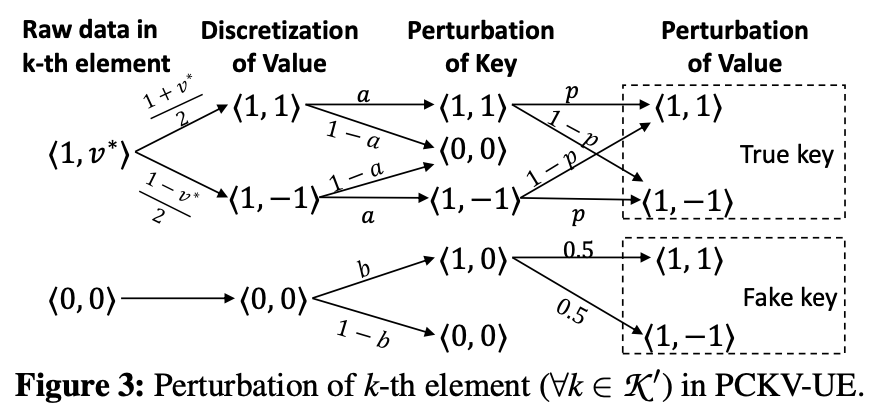
离散化之后，每个 $\langle i, v\rangle \in \{\langle 1, 1\rangle,\langle 1, -1\rangle,\langle 0, 0\rangle\}$，然后呢用一个类似于onehot的方法，可以将 $x=\langle k, v \rangle$ 编码到一个向量 $\bold{x}$，其中第 $k$ 个为 $\langle 1, \pm 1 \rangle $，然后其他位为 $\langle 0,0 \rangle$。那么第 $i$ 个 key perturb 的时候可以有两种，即 $1\rightarrow 1$ 以概率 $a$， $0\rightarrow 1$ 以概率 $b$。然后我们在看 value。

$1 \rightarrow 1$ ：再以概率 $p$ 对 value 进行 RR。
$1\rightarrow 0$ 或者 $ 0 \rightarrow 0$：将值设为 $0$ 。
$0 \rightarrow 1$ ：随机安排值为 1 或者 -1。

这个算法的代码如算法 2 所示，为了方便，我们用 $\{1,-1,0\}$ 表示 $\{\langle 1,1\rangle,\langle 1,-1\rangle,\langle 0,0\rangle\}$。

如果根据最基本的组合性质的话，对 key 的保护是 $\varepsilon_{1}=\ln \frac{a(1-b)}{b(1-a)}$，对 value 的保护是 $\varepsilon_{2}=\ln \frac{p}{1-p}$，那么总的保护是 $\epsilon_1+\epsilon_2$。考虑到 key 和 value 之间的关联性，实际上这个可以有更有的 composition 特性，就是定理2了。

定理2：PCKV-UE 满足 $\epsilon$-LDP，其中：

$\varepsilon=\max \left\{\varepsilon_{2}, \varepsilon_{1}+\ln \left[2 /\left(1+e^{-\varepsilon_{2}}\right)\right]\right\}$

根据这个定理，$\varepsilon \leqslant\left(\varepsilon_{1}+\varepsilon_{2}\right)$，所以这个当中的组合性质是比传统的 composition 更优的（证明过程参考附录A）。

根据这个定理，我们可以这样去分配 $\epsilon_1, \epsilon_2$：

$\varepsilon_{1}=\ln \theta, \quad \varepsilon_{2}=\ln \frac{1}{2 \theta e^{-\varepsilon}-1}, \quad \text { for } \frac{e^{\varepsilon}+1}{2} \leqslant \theta<e^{\varepsilon}$

接下来我们讲解另外一种方法叫PCKV-GRR，类似于GRR的思想，我们只发送一个 kv 对，这就需要在 kv 对之间做一个 perturbation。首先，对于 key $k$ 来说，我们可以规定概率 $a=\frac{e^{\varepsilon_{1}}}{e^{\varepsilon_{1}}+d^{\prime}-1}$为 $k \rightarrow k $ 的概率，然后 $k\rightarrow i(i\not=k)$ 的概率为 $b=\frac{1-a}{d^{\prime}-1}$，这时候 value 的替代被分为了两部分，如果是 $k\rightarrow k$，用 $\epsilon_2$替代，否则随机选取1或者-1。这样，我们就有了 PCKV-GRR算法，如下所示：

对于这个算法，我们可以证明其总的privacy budget是：

$\varepsilon=\ln \left(\frac{e^{\varepsilon_{1}+\varepsilon_{2}}+\lambda}{\min \left\{e^{\varepsilon_{1}},\left(e^{\varepsilon_{2}}+1\right) / 2\right\}+\lambda}\right)$

其中 $\lambda=(\ell-1)\left(e^{\varepsilon_{2}}+1\right) / 2$，证明的过程在附录B中。

Aggregation and Estimation

这一部分对应流程图（图2）中的 4 和 5 两个步骤。数据接收者收到了发送过来的数据之后，首先要统计1的数目和-1的数目。在 PCKV-UE 中，为：$n_{1}=\operatorname{Count}(\mathbf{y}[k]=1), n_{2}=\operatorname{Count}(\mathbf{y}[k]=-1)$，在 PCKV-GRR中，为 $n_{1}=\text {Count}\left(y^{\prime}=\langle k, 1\rangle\right)，n_{2}=\text {Count}\left(y^{\prime}=\langle k, -1\rangle\right)$。然后我们继续用 $n_1,n_2$ 用于进一步计算。参考论文 [23] 中用于 itemset data 的频率估计（当每个用户的 itemset size 小于等于 $l$ 时时无偏的），我们有以下等价的频率估计：

$\hat{f}_{k}=\frac{\left(n_{1}+n_{2}\right) / n-b}{a-b} \cdot \ell$

对应的，均值估计我们用以下式子：

$\hat{m}_{k}=\frac{\left(n_{1}-n_{2}\right) /(2 p-1)}{n \hat{f}_{k} a / \ell}=\frac{\left(n_{1}-n_{2}\right)(a-b)}{a(2 p-1)\left(n_{1}+n_{2}-n b\right)}$

然后，作者给出了定理4用于分析误差：

定理4：假设 padding 的过程中满足每个用户的 $\ell \ge |S_u|$，那么我们有：
$\begin{align} \begin{cases} \mathbb{E}\left[\hat{f}_{k}\right]=f_{k}^{*}\\ \operatorname{Var}\left[\hat{f}_{k}\right]=\frac{\ell^{2} b(1-b)}{n(a-b)^{2}}+\frac{\ell \cdot f_{k}^{*}(1-a-b)}{n(a-b)}\\ \mathbb{E}\left[\hat{m}_{k}\right] \approx m_{k}^{*}\left[1+\frac{(1-b-\delta) b}{n \delta^{2}}\right]\\ \operatorname{Var}\left[\hat{m}_{k}\right] \lesssim \frac{b+\delta}{n \gamma^{2}}+\frac{b(1-b)-\delta}{n \delta^{2}} \cdot m_{k}^{* 2} \end{cases} \end{align}$
其中 $\delta=(a-b) f_{k}^{} / \ell, \quad \gamma=a(2 p-1) f_{k}^{} / \ell$。

上面的估计方法称为 Baseline Estimation Method。其有一定的缺陷，实际上我们可以用 $n_1$ 和 $n_2$ 的结果去估计频率和均值，估计为：

$\left[\begin{array}{l} \hat{n}_{1} \\ \hat{n}_{2} \end{array}\right]=A^{-1}\left[\begin{array}{l} n_{1}-n b / 2 \\ n_{2}-n b / 2 \end{array}\right], \text { where } A=\left[\begin{array}{cc} a p-\frac{b}{2} & a(1-p)-\frac{b}{2} \\ a(1-p)-\frac{b}{2} & a p-\frac{b}{2} \end{array}\right]$

然后我们就可以这么去估计均值：

$\hat{m}_{k}=\ell\left(\hat{n}_{1}-\hat{n}_{2}\right) /\left(n \hat{f}_{k}\right)$

因此对于服务端来说，就可以用以下算法去 Aggregation 了。

Optimized Privacy Budget Allocation

到这里为止，所提出的两个方法都可以 work 了，我们知道给定总的 $\epsilon$ ，我们是分为了 $\epsilon_1$ h和 $\epsilon_2$ 两部分，那么如何去分配使得估计效果更好呢？我们可以顶一个目标，假设总的 $MSE = \alpha \cdot \operatorname{MSE}_{\hat{f}_{k}}+\beta \cdot \operatorname{MSE}_{\hat{m}_{k}}$，使得这个最优即可。然而。根据定理4，$\operatorname{Var}\left[\hat{f}_{k}\right], \operatorname{Var}\left[\hat{m}_{k}\right]$ 是依赖于 $f_{k}^{}, m_{k}^{}$ 的，在 budget allocation 阶段，我们对于这些值是不可知的。因此我们简化这个优化问题。

对于一个估计 $\hat{\boldsymbol{\theta}}$ 来说，MSE可以这么计算：

$\operatorname{MSE}_{\hat{\theta}}=\operatorname{Var}[\hat{\theta}]+\operatorname{Bias}^{2}=\operatorname{Var}[\hat{\theta}]+(\mathbb{E}[\hat{\theta}]-\theta)^{2}$

当 MSE 很大的时候，算法4可以很好地提高估计的效果，因此我们这里分析当MSE相对较小的情况，即：$(2p-1)$ 和 $(a-b)$ 不是特别小的时候，而且 $n$ 比较大的时候。由于一般来说 $f_k^\ll 1$，我们有 $\delta=(a-b) f_{k}^{} / \ell \ll 1$。令：

$\mu=\frac{\ell^{2}}{n f_{k}^{* 2}}, \quad g=\frac{b}{a^{2}(2 p-1)^{2}}, \quad h=\frac{(1-b) b}{(a-b)^{2}}$

那么定理4中的 MSE 可以由以下式子大致给出，其中 $ \mu \ll 1$ 当 $n$ 很大时：

$\begin{aligned} \operatorname{MSE}_{\hat{f}_{k}} &=\operatorname{Var}\left[\hat{f}_{k}\right] \approx \ell^{2} \cdot h / n \\ \operatorname{MSE}_{\hat{m}_{k}} & \approx \mu\left[g+(\mu h+1) h m_{k}^{* 2}\right] \approx \mu\left(g+h \cdot m_{k}^{* 2}\right) \end{aligned}$

我们不难发现，$\operatorname{MSE}_{\hat{m}_{k}}$ 是占大头的，因为频率是基于所有用户的数据估计的，而均值是基于有对应 kv 对的用户估计的。所以当 $\alpha,\beta$ 处于同一量级的时候，我们的优化目标 $MSE = \alpha \cdot \operatorname{MSE}_{\hat{f}_{k}}+\beta \cdot \operatorname{MSE}_{\hat{m}_{k}}$ 可以简化为优化 $\operatorname{MSE}_{\hat{m}_{k}}$。

类似于 OUE 中频率估计的最优解，作者证明了在PCKV-UE中，最优解的配置为：$a=1 / 2, b=1 /\left(e^{\varepsilon_{1}}+1\right), p=e^{\varepsilon_{2}} /\left(e^{\varepsilon_{2}}+1\right)$，即：

$\varepsilon_{1}=\ln \left[\left(e^{\varepsilon}+1\right) / 2\right], \quad \varepsilon_{2}=\varepsilon$

具体的证明过程可以参考附录E部分。

同样的道理，对于PCKV-GRR，我们可以这么分配以达到一个最优解，证明的过程在附录F中：

$\varepsilon_{1}=\ln \left[\ell \cdot\left(e^{\varepsilon}-1\right) / 2+1\right], \quad \varepsilon_{2}=\ln \left[\ell \cdot\left(e^{\varepsilon}-1\right)+1\right]$

其对应的参数为：

$a=\frac{\ell\left(e^{\varepsilon}-1\right)+2}{\ell\left(e^{\varepsilon}-1\right)+2 d^{\prime}}, b=\frac{1-a}{d^{\prime}-1}, p=\frac{\ell\left(e^{\varepsilon}-1\right)+1}{\ell\left(e^{\varepsilon}-1\right)+2}$

我们可以发现，当 $\ell=1$的时候，PCKV-GRR中的分配方案和 PCKV-UE 中的是一样的。总的来说，上面的两个方法的优化可以用图5区表示了。

Evaluation

接下来就到了实验部分了，作者将PCKV-UE 和 PCKV-GRR 与 PrivKVM 和 KVUE 对比。PrivKVM中的参数采用了1r 和 1r5v （1 real iteration and five virtual iterations）两种策略。作者同时测试了生成的数据集和实际数据集。生成的数据集中，一共有 $10^6$ 个用户，$d=100$，同时每个用户仅有一个 KV 对，然后 key 和 value 的分布都服从高斯分布，$\mu=0, \sigma_{\mathrm{key}}=50, \sigma_{\mathrm{mean}}=1$。真实数据集信息如下。

Evaluation Metric采用的是平均MSE，计算如下：

$\mathrm{MSE}_{\mathrm{freq}}=\frac{1}{|X|} \sum_{i \in X}\left(\hat{f}_{i}-f_{i}^{*}\right)^{2}, \quad \operatorname{MSE}_{\mathrm{mean}}=\frac{1}{|X|} \sum_{i \in X}\left(\hat{m}_{i}-m_{i}^{*}\right)^{2}$

Synthetic Data

我们先来看一下生成数据集上不同方法的表现。

首先看了一下不同的分布对实验结果的影响，可以看到总的来说的话所提出的方法较为优秀。

然后作者测试了不同的 domain size，总的来说依然是所提出的方法较好。

接着作者看了一下top10和top20的准确率随着domain size的变化，结果如上所示。

Real-Wrold Data

上述是在生成的数据集上的实验，在生成的数据集上，作者所提出的方法依然有着不错的表现。

Conclusion

本文提出了一个新的框架叫做 PCKV 同时提出了两种用于 KV perturbation 的方法。相对于sequential composition，本文所提出的方法具有 tighter budget composition 。本文依然遗留一个问题，即如何更优地去设置 $\ell$ 使得效果更好。

Appendix A

为了方便，我们把算法1放过来：

同时也把 PCKV-UE 放过来：

对于一个用户的 Key-Value 对集合 $S$，其可以表示成 $\langle i, v_i^\rangle$ 的集合，$i$ 表示 $\langle i, \cdot \rangle$ 存在于 $S$ 中。根据算法1中的第5行，如果采样的是 dummy，那么 $v_k^=0 $的。因此这个算法的输入向量中，只有第 $k$ 个是 1 或者 -1，其他都是 0。那么输出的概率为：

$\begin{aligned} \operatorname{Pr}(\mathbf{y} | S, k) &=\operatorname{Pr}\left(\mathbf{y}[k] | v_{k}^{*}\right) \prod_{i \in K^{\prime} | k} \operatorname{Pr}(\mathbf{y}[i] | \mathbf{x}[i]=0) \\ &=\frac{\operatorname{Pr}\left(\mathbf{y}[k] | v_{k}^{*}\right)}{\operatorname{Pr}(\mathbf{y}[k] | \mathbf{x}[k]=0)} \cdot \prod_{i \in K^{\prime}} \operatorname{Pr}(\mathbf{y}[i] | \mathbf{x}[i]=0) \end{aligned}$

根据PCKV-UE流程，前一部分为：

$\operatorname{Pr}\left(\mathbf{y}[k] | v_{k}^{*}\right)=\left\{\begin{array}{ll}\frac{1+(2 p-1) v_{k}^{*}}{2} \cdot a, & \text { if } \mathbf{y}[k]=1 \\ \frac{1-(2 p-1) v_{k}^{*}}{2} \cdot a, & \text { if } \mathbf{y}[k]=-1 \\ 1-a, & \text { if } \mathbf{y}[k]=0\end{array}\right.$

为了方便，我们取以下两个符号：

$\Psi(\mathbf{y}, k)=\frac{\operatorname{Pr}\left(\mathbf{y}[k] | v_{k}^{*}\right)}{\operatorname{Pr}(\mathbf{y}[k] | \mathbf{x}[k]=0)}, \quad \Phi(\mathbf{y})=\prod_{i \in K^{\prime}} \operatorname{Pr}(\mathbf{y}[i] | \mathbf{x}[i]=0)$

那么有：$\operatorname{Pr}(\mathbf{y} | \mathcal{S}, k)=\Psi(\mathbf{y}, k) \cdot \Phi(\mathbf{y})$，同时：

$\Psi(\mathbf{y}, k)=\left\{\begin{array}{ll}\left(1+(2 p-1) v_{k}^{*}\right) \cdot \frac{a}{b}, & \text { if } \mathbf{y}[k]=1 \\ \left(1-(2 p-1) v_{k}^{*}\right) \cdot \frac{a}{b}, & \text { if } \mathbf{y}[k]=-1 \\ \frac{1-a}{1-b}, & \text { if } \mathbf{y}[k]=0\end{array}\right.$

接下来我们分类讨论：

Case 1 ：对于 $k\in\{1,2…,d\}$，我们有 $v_k^*\in[-1,1]$，并且

$\frac{1-a}{1-b} \leqslant \frac{2 p a}{b}, \quad \frac{2(1-p) a}{b} \leqslant\left(1 \pm(2 p-1) v_{k}^{*}\right) \cdot \frac{a}{b} \leqslant \frac{2 p a}{b}$

所以：

$\Psi_{\text {upper }}=\frac{2 p a}{b}, \quad \Psi_{\text {lower }}=\min \left\{\frac{1-a}{1-b}, \frac{2(1-p) a}{b}\right\}$

Case 2 ：对于 $k\in\{d+1, …, d’\}$，我们有 $v_k^*=0$，我们有：

$\Psi_{\text {upper }}^{\prime}=\frac{a}{b}, \quad \Psi_{\text {lower }}^{\prime}=\frac{1-a}{1-b}$

注意到，我们有：$
\Psi_{\text {lower }} \leqslant \Psi_{\text {lower }}^{\prime} \leqslant \Psi_{\text {upper }}^{\prime} \leqslant \Psi_{\text {upper }}$，那么我们就能计算出：

$\begin{array}{l}\operatorname{Pr}(\mathbf{y} | S)=\eta \sum_{k \in S} \frac{\operatorname{Pr}(\mathbf{y} | S, k)}{|S|}+(1-\eta) \sum_{k=d+1}^{d^{\prime}} \frac{\operatorname{Pr}(\mathbf{y} | S, k)}{\ell} \\ =\Phi(\mathbf{y})\left[\frac{\eta}{|S|} \sum_{k \in S} \Psi(\mathbf{y}, k)+\frac{1-\eta}{\ell} \sum_{k=d+1}^{d^{\prime}} \Psi(\mathbf{y}, k)\right] \\ \leqslant \Phi(\mathbf{y})\left[\frac{\eta}{|S|} \cdot|S| \Psi_{\text {upper }}+\frac{1-\eta}{\ell} \cdot \ell \Psi_{\text {upper }}^{\prime}\right] \leqslant \Phi(\mathbf{y}) \cdot \Psi_{\text {upper }}\end{array}$

再根据 LDP 的定义，我们有：

$\begin{array}{l}\frac{\operatorname{Pr}\left(\mathbf{y} | S_{1}\right)}{\operatorname{Pr}\left(\mathbf{y} | S_{2}\right)} \leqslant \frac{\Phi(\mathbf{y}) \cdot \Psi_{\text {upper }}}{\Phi(\mathbf{y}) \cdot \Psi_{\text {lower }}}=\frac{\Psi_{\text {upper }}}{\Psi_{\text {lower }}}=\frac{2 p a / b}{\min \left\{\frac{1-a}{1-b}, \frac{2(1-p) a}{b}\right\}} \\ =\max \left\{2 p \cdot \frac{a(1-b)}{b(1-a)}, \frac{p}{1-p}\right\}=\max \left\{\frac{2 e^{\varepsilon_{1}}}{1+e^{-\varepsilon_{2}}}, e^{\varepsilon_{2}}\right\}=e^{\varepsilon}\end{array}$

所以这个定理就证明完毕了。

本篇内容到这里就结束了，欢迎关注公众号《差分隐私》，获取更多前沿技术。

《差分隐私》